a junction tree not that uglily displayed{.imagelink}

I updated the graph display component to produce better results.

It already featured a gradient descent + basic simulated reheat. The problem with this method is that the speed of convergence to an acceptable minimal display cost depends heavily on the initial solution (especially true for large graphs). As I don’t expect the user to wait until a good solution is found, I added a heuristic used to build an initial solution that will require only a fixed amount of gradient descents to be “smoothed”.

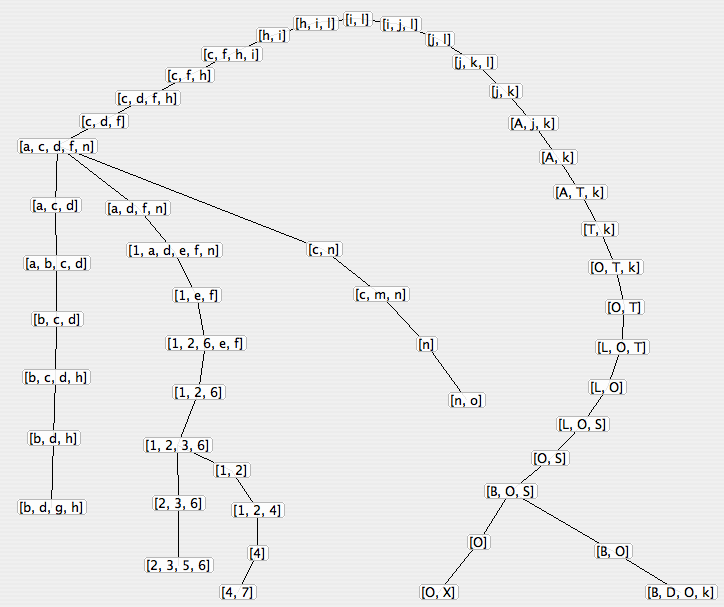
The main idea is to measure the “rootness” of a node. This rootness is more or less the number of steps you would have to make from this node to reach all the nodes if they were placed in circles around this node.

Using this rootness, I define a “power” of each node. Basically, between two nodes with equal rootnesses, the one that has the greatest power is the one that has the most neighbours. The formula is actually recursive, so that nodes more central than some powerful nodes kind of inherit a part of their power.

Once I have the power of all nodes, I sort them by decreasing power. Then there are two options :</p>

  • trees : create as many rows as there are different power values. In each row, find the best position for each node between a fixed set of possible positions. Assign these positions on a first arrived, first served basis, the first served being the nodes with the greatest power
  • non-trees : use the same algorithm as for trees, but organizing concentric circles instead of rows

Once this “rigid” assignment of nodes to predefined positions is done, I run a fixed amound of gradient descents with a very small descent factor, just to smooth the graph. This gives incredible results in an amount of time constant for a given graph.

[Edit Oct. 9th 2006] : it looks like Bayesia is selling a tool which sole purpose is to do graph layouts… They’re apparently using genetic algorithms and it would be worth having a look at all the parameters they allow the user to integrate to the cost functions… and to have an idea of the time it takes them to get a decent solution !