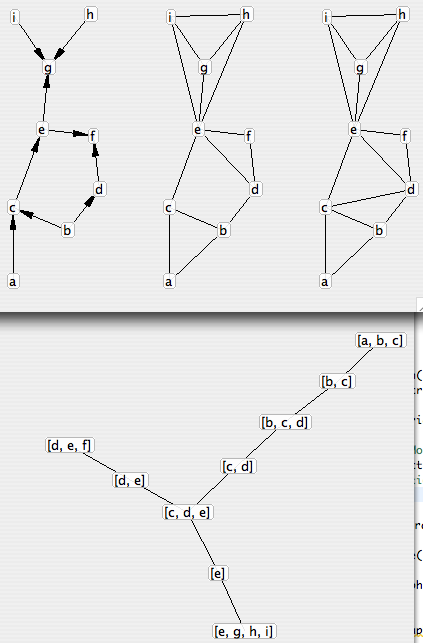
Graphs : minimal junction tree
Tonight I implemented Kruskal’s minimal spanning tree algorithm (arbre couvrant minimal) in my graph library.</p>
This allowed me to add computation of the minimal junction tree of a directed graph (as explained on Wikipedia : minimal spanning tree of the junction graph of the triangulated moralization of this graph, each edge in the spanning tree being weighted with minus the size of the intersection of the two cliques or separator of that edge).</p>
The result speaks for itself :</p>
While in the subway I also found a way to represent data collected during training of a fixed-architecture bayesian network. The goal is to be able to set and retrieve the Nijk as defined in the statistical training of bayesian networks (number of times the node Xi was in state k and parents of Xi were in state j at the same time). For each random variable X with parents pa(X) in the bayesian network, I define an unique ordering Nx over the definition set of { X } U pa(X) and an unique ordering Mx over the definition set of pa(X). Mx gives me the j index (a unique integer for each possible instantiation of pa(X)). The k index is obvious to get (it is over a single variable). For each sample, for each node we put in a database an entry with { sampleId, nodeId, Nx(sample), Mx(sample) }.</p>
When we calculate the likeliness maximum (maximum de vraisemblance) :
| p(Xi = xk | pa(Xi) = xj) = Nijk / Sum(k’, Nijk’) |
then we can get all the Nijk’ coefficients by issuing the query { nodeId == i AND Nx(sample) == Nx(xk, xj) } to the database of samples.</p>
Next steps :</p>
- finalize the likeliness table implementation
- implement the inference in the minimal junction tree
- test instantiation and marginalization with examples from wikipedia, and my book
- implement statistical training over complete data sets
- implement bayesian training over incomplete data sets, possibly using statistical estimations of parameters as a priori